Начальный вариант игры «Геометрика»
Этот вариант можно использовать для игры с маленькими детьми или для начального знакомства с игрой.
В игре используются колода с фигурами и колода с признаками. В обеих колодах карты промаркированы точками (от одной до трёх) по уровню сложности. Для начала можно использовать в игре только карты с одной точкой.
Первый игрок берет карту из колоды признаков. Ему нужно найти среди выложенных фигур такую, которая соответствует хотя бы одному из двух признаков на его карте.
Если ему это удаётся — он забирает себе карту признаков и соответствующую ей фигуру в свою стопку. Если его карте признаков соответствует две или три фигуры, то игрок всё равно забирает только одну фигуру (любую на свой выбор). На стол из колоды фигур выкладывается новая фигура, чтобы фигур было по-прежнему три, ход переходит следующему игроку.
Если игрок не может найти фигуру, соответствующую своей карте с признаками, то эта карта с признаками уходит в «отбой», ход также переходит следующему по очереди.
Когда колода признаков заканчивается — игроки подсчитывают набранные карты. Кто набрал больше карт — тот и победил!
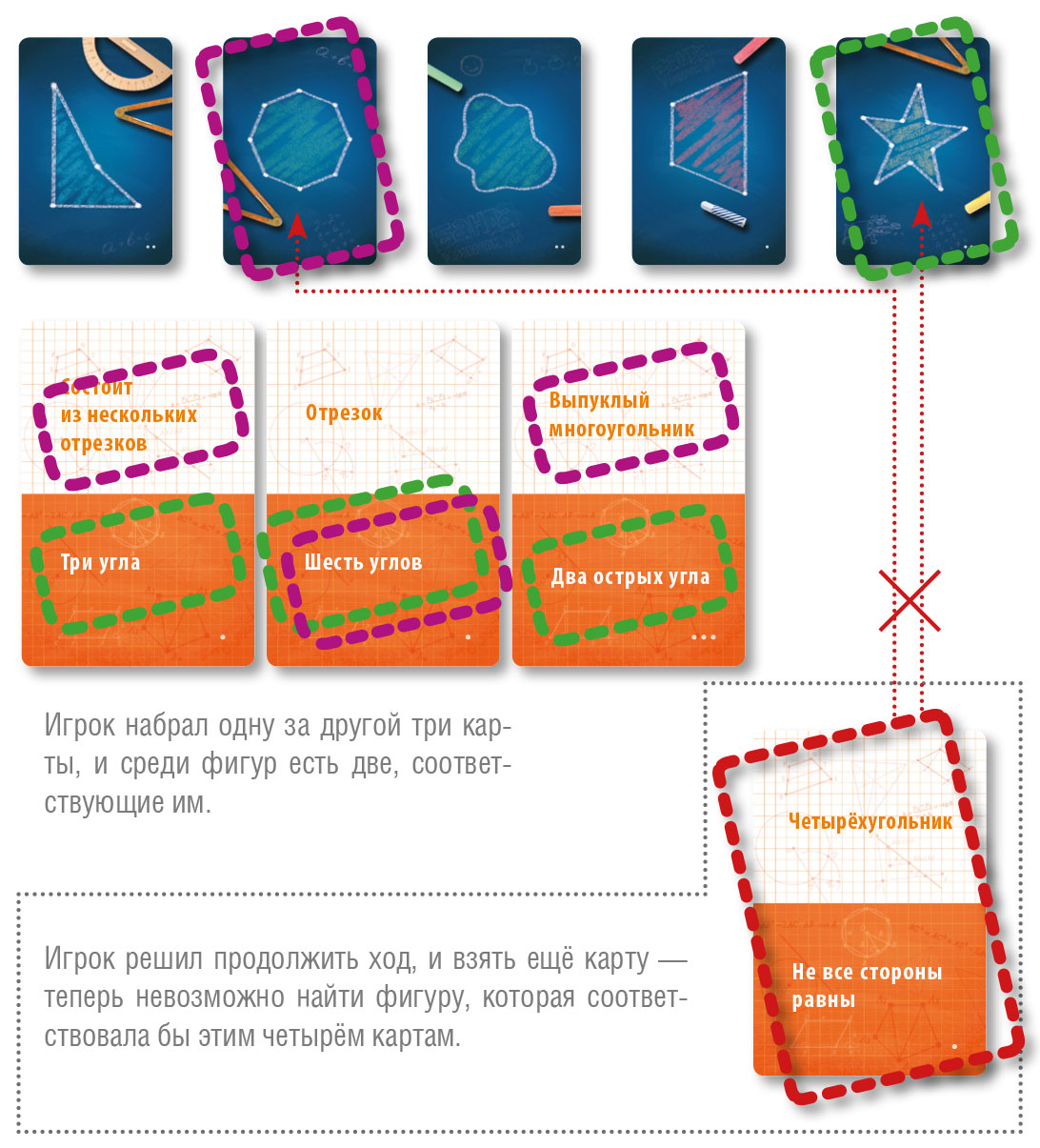
Основной вариант игры «Геометрика»
В основном варианте игры на стол выкладываются пять фигур, игроки ходят по очереди. Теперь задача игрока за свой ход набрать как можно больше карт признаков и вовремя остановиться, чтобы не случился «перебор».
Взяв карту, игрок должен найти среди выложенных фигур такую, которая соответствует взятой им карте признаков. На карте есть два признака: игрок выбирает любой из них на своё усмотрение (второй признак при этом игнорируется).
Если игрок находит подходящую фигуру — он может:
- Завершить ход, забрав в свою стопку карту признаков и одну соответствующую ей фигуру.
- Продолжить ход, взяв ещё одну карту с признаками. Теперь ему нужно найти фигуру, соответствующую обеим картам. То есть фигура должна одновременно соответствовать какому-то признаку на первой карте и какому-то признаку на второй карте.
Верхнему признаку соответствует одна фигура, нижнему — ещё две фигуры. Игрок может:
- либо завершить ход, забрав карту с признаками и одну из этих трёх карт с фигурами (любую на свой выбор);
- либо продолжить свой ход — тогда он берёт из колоды ещё одну карту с признаками.
Каждый раз, удачно взяв карту, игрок решает, брать ли следующую (рискуя получить «перебор») или завершить ход (забрав набранные карты признаков и одну соответствующую им фигуру). Вместо забранной фигуры каждый раз из колоды добавляется другая, чтобы на столе оставалось пять фигур.
Если же игрок, взяв очередную карту, не может найти подходящую фигуру — он объявляет «перебор»: все набранные им в этот ход карты признаков уходят в «отбой», ход завершается.
Что есть что:
- Равносторонний треугольник — у него все стороны и все углы равны.
- Равнобедренный треугольник — равны хотя бы две стороны, поэтому фигура симметрична; равносторонний треугольник тоже является равнобедренным.
- Прямоугольный треугольник — один угол у треугольника прямой.
- Четырёхугольник — любая фигура с четырьмя углами, включая четырёхугольник с вогнутым углом, квадрат, прямоугольник, ромб, параллелограмм, трапецию.
- Квадрат — четырёхугольник, у которого все стороны равны, а все углы прямые.
- Прямоугольник — четырехугольник, у которого все углы прямые, а противоположные стороны равны; любой квадрат тоже является прямоугольником.
- Ромб — четырёхугольник, у которого все стороны равны; квадрат тоже является ромбом.
- Параллелограмм — четырёхугольник, у которого противолежащие стороны равны; ромб, квадрат и прямоугольник тоже являются параллелограммами.
- Трапеция — четырёхугольник, у которого две стороны параллельны, а две другие — нет; поэтому квадрат, прямоугольник, параллелограмм и ромб не являются трапецией.
- Пятиугольник (и любой скольки-то угольник) включают выпуклые и вогнутые фигуры; например, пятиконечная звезда является десятиугольником — у неё 5 выпуклых (концы лучей) и 5 вогнутых (у оснований лучей) углов.
- Правильный многоугольник — все стороны равны и все углы равны.
- Выпуклый многоугольник — все углы меньше 180 градусов (не вогнутые).
- Вогнутый многоугольник — содержит хотя бы один вогнутый угол.
- Эллипс — фигура, похожая на овал («сплющенный круг»).
- Отрезок — две точки, соединенные между собой прямой линией.
- Луч — прямая линия, имеющая начальную точку, но не имеющая конечной точки, и поэтому она бесконечно продолжается в одну из сторон (на карте уместился только начальный участок луча).
- Прямая — прямая линия, не имеющая начальной и конечной точки, и продолжающаяся бесконечно в обе стороны (на карте уместилась только маленькая часть прямой).
- Незамкнутая ломаная линия — состоит из нескольких соединённых отрезков.
- Незамкнутая плавная кривая — не прямая, не имеет углов, имеет не совпадающие начало и конец.
- Зеркальная симметрия — через фигуру можно провести линию так, что слева и справа от неё будут зеркально одинаковые половины. Такой симметрией обладает, например, равнобедренный треугольник или буква «Т».
- Периметр — контур замкнутой фигуры.
- Конечный размер — свойство, подразумевающее принципиальную измеримость фигуры. Например, луч и прямая — объекты, которые простираются на неограниченное расстояние, и не имеют конечного размера.
- Острый угол — угол меньше 90 градусов (более «острый», чем прямой угол)
- Прямой угол — угол 90 градусов
- Тупой угол — угол от 90 до 180 градусов
- Развёрнутый угол — угол в 180 градусов, лучи угла «раскладываются» при этом в единую прямую.
- Вогнутый угол (такой угол может быть только у замкнутого многоугольника) — угол больше 180 градусов, он как бы «вогнут» внутрь фигуры.
Вопросы по формулировкам?
Формулировки на картах трактуются буквально.
«Не все стороны равны» — у фигуры есть больше одной стороны (например, под определение не подходит отрезок или круг), и их длина неодинакова (например, прямоугольник или любой неравносторонний треугольник).
«Все стороны разные по длине» — у фигуры больше одной стороны, и ни одна из них не одинакова с какой-либо другой по длине.
Видеообзор игры «Геометрика»
- Подразумевается трактовка с позиции «как минимум», например:
- «Четыре угла» — у фигуры как минимум четыре угла, но может быть и больше. А вот под формулировку «Ровно четыре угла» подходят только фигуры, у которых именно и только четыре угла.
«Вогнутый угол» — у фигуры есть хотя бы один вогнутый угол, но их может быть и больше (например, у пятиконечной звезды). «Три стороны равны» — хотя бы три стороны равны, но может быть и больше равных сторон (например, у правильного восьмиугольника).
- Подразумевается буквальное наличие признаков, например:
